Modeling Black-Litterman; Part 1 - Reverse Optimization

 "The 'radical' of one century is the 'conservative' of the next."

-Mark Twain

In this series, I'm going to explore some of the advances in portfolio management, construction, and modeling since the advent of Harry Markowitz's Nobel Prize winning Modern Portfolio Theory (MPT) in 1952.

MPT's mean-variance optimization approach shaped theoretical asset allocation models for decades after its introduction.  However, the theory failed to become an accepted industry practice, so we'll explore why that is and what advances have developed in recent years to address the shortcomings of the original model.

The Problems with Markowitz

For the purpose of illustrating the benefits of diversification in a simple two-asset portfolio, Markowitz's model was a useful tool in producing optimal weights at each level of assumed risk to create efficient portfolios.  

However, in reality, investment portfolios are complex and composed of large numbers of holdings across asset classes and when MPT is applied in practice, the results raise three notable issues.

1. First, MPT suffers from a hyper-sensitivity to input assumptions.  While not highly dependent on the risk factor inputs from the variance-covariance matrix, model outputs can swing wildly from even small changes to the expected return input vector.                                                              
2. The second issue becomes evident in long-only constrained model portfolios... MPT has a tendency to produce highly concentrated asset weightings and the intended diversification benefits are lost in the process.                                                                                                                           
3. Lastly, Markowitz's model depends on the assumption that all inputs are known which leads to the issue of estimation error.  Outcomes of events follow distribution patterns, most commonly the normal distribution, which makes accurately forecasting any result on a consistent basis a statistical impossibility.

Black-Litterman

To address these issues, two Goldman economists, Fischer Black and Robert Litterman, built on the work of Markowitz to produce the first incarnation of the Black-Litterman model in 1990.

Their new approach, which gained recognition throughout the industry in the early 2000s, overcame the shortcomings of MPT by using market-implied inputs, incorporating manager insights and dispersing forecast errors among the input variables.

Reverse Optimization

To address the issues of input sensitivity, Black and Litterman ultimately moved away from the optimization process of MPT to produce portfolio weights as the model output.  Instead, they built on the aspect of the investor utility-maximization principle which assumes that the market portfolio is mean-variance efficient and therefore the observable portfolio weights, in the form of asset allocations, already represent the optimal portfolio.

Utility maximization states that investors, when presented with investment options that are perfect compliments of each other, will maximize their utility at the point of indifference between a combination of perfectly complimenting investible assets.

where:

From there, they used a reverse optimization process to determine the market-implied expected excess return for each asset class.  Because utility is maximized at the indifference point of consumption between perfect compliments, the function is solved by setting the combination of assets to zero.

where:

Building the Market Portfolio

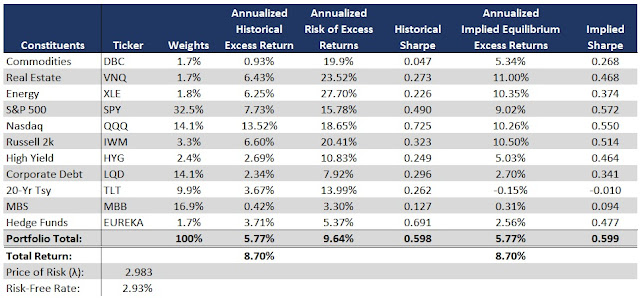
In order to illustrate the Black-Litterman process, we first have to construct a market portfolio.  To do this, I built a U.S.-based portfolio consisting of traditional and alternative asset classes that have sufficient transparency while trying to maintain mutual exclusivity.

Here's what I came up with:

Let's be very clear, the purpose of this exercise is not to construct the perfect U.S. market portfolio, so we remain cognizant that this model is a proxy for an actual market portfolio... we're ultimately trying to find the best combination of simplicity of variable inputs and market depth here.  

It is useful to note the following, however:

• Energy, Real Estate, & Commodities/Materials weights have been subtracted from the S&P market cap weight

• Domestic hedge fund exposure is approximated to be roughly equal to the size of the real estate market and performance is taken from Eurekahedge global benchmark

• The use of TLT (20-year Treasury ETF) as a measure of Treasury performance is not ideal as it's a long-duration ETF, but is considered the best proxy based on an assumption of an indefinite investment horizon and the choice of a shorter-term risk-free rate

• There is a conspicuous absence of private equity, infrastructure and real assets due to data limitations

Pricing Risk

Now that we have our model market portfolio, we can calculate the implied market price of risk by solving for lambda.  Lambda is a risk-aversion coefficient that describes the required excess return relative to risk... investors with higher risk-aversions will require greater excess return to assume additional risk and vice versa.

In this model, we are using 15 years of monthly returns and the 10-year treasury yield is the risk-free rate.

We noted earlier that lambda is equal to the portfolio expected excess return divided by two times the variance of the raw portfolio returns.

• The monthly average excess return for our market portfolio is 0.462%

• The variance of the raw monthly returns is 0.077%

• Which produces a portfolio lambda of 2.983

A lambda value approaching 3 seems considerably high and we have to recall what the time period we're using includes the last 15 years - starting in June of 2007 - which has seen anomalous growth resulting from unprecedented levels of monetary and fiscal stimulus.  This time period also includes two volatility shocks resulting from the financial crisis and the Covid crash; however, outside of these two events, volatility has been prosaic.

Is it realistic to assume markets will experience similar levels of risk-adjusted growth in the future as they've experienced in these last 15 years?  Probably not... but that's the beauty of modeling, we can always adjust the lambda value to see the effects of changing assumptions.

For starters though, we'll use the calculated lambda value of 2.983.

Market Implied Excess Return

We saw before that the implied excess return is equal to the product of two, lambda, the variance-covariance matrix of excess returns, and the market weights.

Below, we see a comparison between the historical asset returns and the implied asset returns calculated by reverse optimization:

The differences between historical returns and implied returns are notable among many of the assets but more interesting is the fact that the average of the implied vector return's is higher than the historical return vector and with a lower dispersion.

Model Output

(click on image to enlarge)

Here's the overall output from the reverse optimization process (image size is limited on Blogger now).  Where this really gets interesting is when we use the new expected return vector in a Markowitz style mean-variance optimization.

Here, we see the Markowitz-produced efficient frontier well above the Black-Litterman frontier as the MPT approach produces higher excess return portfolios.  However, the criticism of the Markowitz model was sector concentration.

Below, we see the asset allocations for each model at the 10% vol portfolio:

(click on image to enlarge)

The Markowitz 10% vol portfolio has an expected excess return of 8.57% vs 5.98% for Black-Litterman.  However, the biggest difference is in asset concentration.  The Markowitz model is confined to just three asset classes - large cap growth, treasuries, and hedge funds.  Meanwhile, the Black-Litterman portfolio is comprised of 9 out of a possible 10 total allocations.

*References:     Microsoft Word - BL Draft with Graphs.doc (duke.edu)

                    Phil Davies - YouTube